Tra le coniazioni più interessanti volute dall’Università di Padova ce n’è una, modernissima, per i quattro secoli dalla morte filosofo Giacomo Zabarella
di Roberto Ganganelli | “Giacomo Zabarella, chi era costui?” Parafrasando l’adagio manzoniano, andiamo a conoscere – grazie ad una medaglia che è anche un esempio d’arte contemporanea – uno dei pensatori italiani più importanti del XVI secolo, nato a Padova nel 1533 e morto ancor giovane nella città veneta, nel 1589.
Conte palatino, cavaliere e… filosofo
Primogenito di un’aristocratica famiglia, Giacomo Zabarella eredita dal padre Giulio il titolo di conte palatino e si laurea in filosofia naturale a vent’anni senza tuttavia abbinare questo titolo, a differenza di tanti suoi contemporanei, ad una formazione sistematica in medicina.

La sua carriera universitaria a Padova inizia nel 1563 o nel 1564, dapprima con l’insegnamento della logica e in seguito con quello della filosofia naturale passa alla storia la controversia che lo vede opposto a Francesco Piccolomini e Bernardino Petrella a proposito della struttura logica della scienza e dell’ordine secondo la quale essa viene acquisita.
Allievo di Francesco Robortello, Marcantonio de’ Passeri e Bernardino Tomitano, nell’anno accademico 1563-1564 Giacomo Zabarella succede a quest’ultimo nella cattedra di logica. Per l’anno accademico 1568-1569 ottenne la seconda cattedra di filosofia naturale straordinaria e per l’anno accademico 1577-1578 ottenne la prima di filosofia naturale straordinaria, che mantiene fino all’anno accademico 1584-1585. Nel successivo ottiene poi la seconda cattedra di filosofia naturale ordinaria, che occupa fino alla morte, nel 1589.

Esponente dell’aristotelismo, conoscitore della lingua greca al punto da poter leggere le opere in originale, Zabarella redige una serie di commentari al grande pensatore classico e numerosi studi di logica, che vengono pubblicati sotto il titolo di Opera logica; redige inoltre trattati di filosofia naturale raccolti nel De rebus naturalibus.
Richiamandosi alla distinzione, tipicamente aristotelica, fra artes e scientiae, Giacomo Zabarella sostiene che la logica non è una scienza né un’arte, ma piuttosto uno strumento al servizio delle arti e delle scienze, il cui scopo consiste nel distinguere il vero dal falso.
Il filosofo si pone anche il problema della metodologia da impiegare in ambito scientifico, individuando un “metodo risolutivo” e un “metodo compositivo”: il primo parte dall’esame dei fenomeni per risalire alla ricerca delle cause; il secondo, invece, partendo dall’esame mentale della causa, giunge alla spiegazione scientifica del fatto percepito. Zabarella propone quindi una combinazione dei due metodi , dando luogo al cosiddetto “metodo del regresso”.
La medaglia di Giò Pomodoro per l’Università di Padova
Passano quattro secoli dalla scomparsa di Giacomo Zabarella e lo Studium patavinum – quello stesso ateneo che compie quest’anni otto secoli di vita e a cui l’Italia ha dedicato una moneta da 5 euro – ricorda il filosofo con una medaglia celebrativa, coniata da Johnson in bronzo dorato nel diametro di 57-62 millimetri
A idearla è Giò Pomodoro (1930-2002), famoso scultore, orafo e incisore esponente di punta dell’astrattismo del XX secolo e fratello dell’altrettanto noto Arnaldo (1926).
La medaglia, dal profilo assolutamente irregolare – c’è chi l’ha irrispettosamente definita “un uovo al tegamino” – sembra parafrasare la materia informe, la natura dallo sviluppo in apparenza caotico e privo di schemi definiti e formalizzabili.

All’interno della curiosa sagoma, tuttavia, sia al dritto che al rovescio si evidenzia un profilo perfettamente circolare che ospita, al suo interno, una complessa composizione di armoniose figure geometriche (in rilievo al dritto) basate sul concetto della sezione aurea.

Definita da Keplero come “uno dei due grandi tesori della geometria” (l’altro è il teorema di Pitagora), la seziona aurea – nota già nell’antichità – venne formalizzata dai pitagorici come rapporto tra la diagonale e il lato di un pentagono regolare.
Il rapporto aureo in natura e nelle arti
Indicato tradizionalmente con la lettera greca Φ (l’iniziale del nome di Fidia), il rapporto aureo venne definito tale in quanto appariva come il più “estetico” ed “armonioso” tra quelli possibili per i lati di un rettangolo. Pare che tale rapporto, pari a ( , ossia a 1,618033…, fosse noto già agli Egizi, che su di esso impostarono le proporzioni delle piramidi; proporzioni che, analoghe, si ritrovano anche nel Partenone e in alcune architetture monumentali di epoche successive.
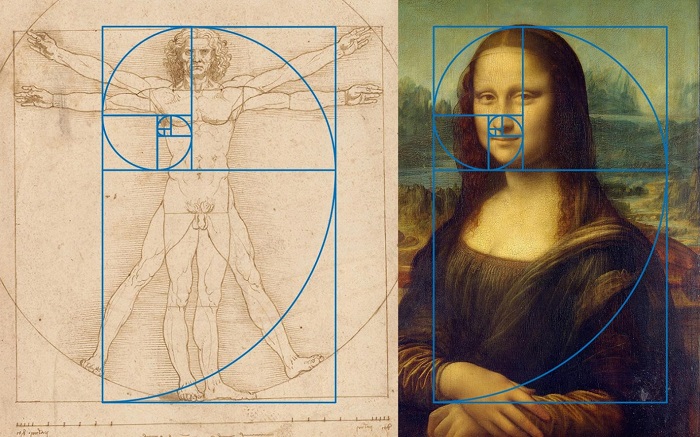
Nella pittura e nella scultura, la sezione aurea ha avuto un ruolo fondamentale definendo ad esempio, nel Rinascimento, le proporzioni di raffigurazione di paesaggi e figure umane (come non ricordare l’Uomo vitruviano di Leonardo, in cui l’altezza dell’individuo è divisa in modo “aureo” dalla posizione dell’ombelico?). In tempi più recenti, è toccato a Piet Mondrian rinverdire i fasti del rettangolo aureo in varie delle sue opere, basate appunto sulla composizione di quadrati e rettangoli.
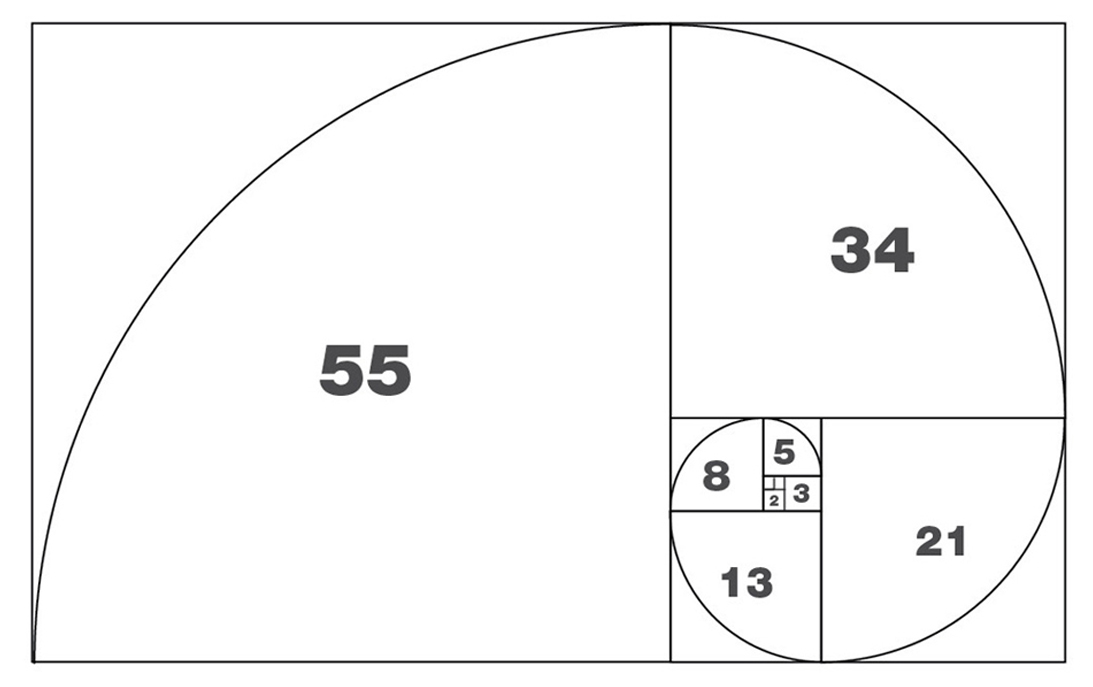
Alla sezione aurea sono correlati i numeri di Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34 ecc…), quella successione in cui ogni numero intero è dato dalla somma dei due precedenti. Se si procede nella generazione dei termini, infatti, si nota come il rapporto tra due consecutivi si avvicini sempre più (e, all’infinito, coincida) proprio con il “magico” valore della sezione aurea, protagonista nei secoli di infiniti utilizzi simbolici e pratici.
I numeri di Fibonacci, e quindi la sezione aurea, si ritrovano anche in natura, ad esempio nel numero delle spirali dei semi del girasole, dei petali di alcuni fiori, nelle scaglie dell’ananas.
La fllotassi, ossia lo studio della disposizione geometrica di foglie e infiorescenze, ha rivelato inoltre che alcune piante dispongono le loro foglie sul fusto secondo quella che è definita una “spirale vegetativa” ad angoli costanti, pari all’angolo aureo di 137,5 gradi, utilizzando così in maniera ottimale la luce solare.
La logica nascosta, la perfezione della geometria
Ecco che si spiega, dunque, l’accostamento della sezione aurea al filosofo Giacomo Zabarella sulla bellissima medaglia di Pomodoro il cui dritto anepigrafe – un vero e proprio bassorilievo moderno – sembra porre l’accento sul caos apparente della natura che, agli occhi dello studioso, rivela tuttavia la sua logica nascosta, le inattese regolarità celate e la perfezione dei rapporti fissi della geometria.
A ribadire questo concetto, sul rovescio della medaglia per Giacomo Zabarella, ritornano le linee fondamentali del rettangolo e della spirale aurea, del cerchio e dei suoi diametri abbinate al nome dell’Università di Padova, del personaggio e ad una quanto mai azzeccata epigrafe in latino che recita NIHIL UNQUAM SINE RATIONE (“Mai senza un motivo”).







































